七大排序算法分析及java实现
2020-12-13 06:23
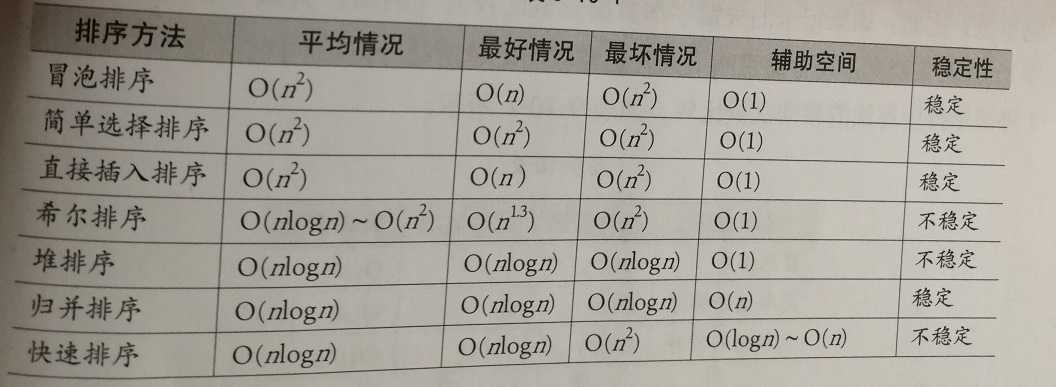
标签:开始 int 构建 qsort 复杂 记录 sort 难题 turn 知识点: 排序分为内排序和外排序。内排序是在排序整个过程中,待排序的所有记录全部被放置在内存中。外排序是由于排序的记录个数太多,不能同时放置在内存,整个排序过程需要在内外存之间多次交换数据才能进行。这里主要介绍内排序: 内排序可分为四种,交换排序、选择排序、插入排序、归并排序。 排序的稳定性: 若k为记录的排序字段且ki=kj,排序前ki所表示的记录排在kj所表示的记录前面,排序后若顺序保持不变,则为稳定排序,若排序后ki,kj顺序发生变化,则为不稳定排序。 七种排序算法性能归纳比较: 1、冒泡排序 最好情况下(待排序表顺序),进行n-1次比较,没有交换,时间复杂度为O(n) 最坏情况下(待排序表逆序),比较和交换次数相等,为1+2+3+……+(n-1) = n*(n-1)/2,时间复杂度为O(n2) 2、简单选择排序 特点:交换次数少 无论最好最坏情况,比较1+2+3+……+(n-1)+(n-2)=n*(n+1)/2次,时间复杂度O(n2) 最好情况下交换0次,最差情况下交换n-1次 尽管与冒泡排序时间复杂度同为O(n2),但其性能略优于冒泡排序 3、直接插入排序 最好情况,比较n-1次,交换0次,时间复杂度为O(n) 最坏情况,比较2+3+4+……+n=(n-1)*(n-2)/2次,交换3+4+……+(n+1)=(n-1)*(n+4)/2次 4、shell排序 increment如何选取是一个尚未解决的数学难题 5、堆排序 堆排序的运行时间主要消耗在初始构建堆和反复筛选堆上,初始构建是从二叉树最下层最右边非终端节点开始。对每个非终端节点来说,最多进行两次比较和互换,时间复杂度为O(n)。 正式排序时,第i次取堆顶,重建堆要用O(nlogi) (完全二叉树某节点到根节点距离为[log2i] +1,并且需要取n-1次堆顶),因此时间复杂度为O(nlogn)。 6、归并排序 递归实现: 非递归实现: 一趟归并需要将长度为n的序列进行两两归并,时间复杂度为O(n),二叉树深度为[logn]+1,因此时间总复杂度为O(nlogn) 递归法空间复杂度为归并过程中用到的原始数组的副本O(n)及递归栈log2n, 非递归方法的空间复杂度为O(n) 7、快速排序 最好情况时间复杂度O(nlogn),最差为O(n2) 最好情况下空间复杂度为O(logn),最差情况下空间复杂度为O(n),平均复杂度为O(logn) 快排整体性能优越,但排序不稳定,需要大量辅助空间,对少量数据排序无优势 数据基本有序情况下,不考虑四种复杂排序算法 七大排序算法分析及java实现 标签:开始 int 构建 qsort 复杂 记录 sort 难题 turn 原文地址:https://www.cnblogs.com/javaXRG/p/11173662.html
交换排序
选择排序
插入排序
归并排序
冒泡排序
快速排序
简单选择排序
堆排序
简单插入排序
shell排序
归并排序
1 public class BubbleSort {
2
3 public static void main(String[] args) {
4 int[] array = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
5 bubbleSort(array);
6 System.out.println(Arrays.toString(array));
7 }
8
9 public static void bubbleSort(int[] array) {
10 boolean flag = true;
11 for(int i = 0; i ) {
12 flag = false;
13 for(int j = array.length - 1; j > i; j--) {
14 if(array[j] ]) {
15 swap(array, j, j - 1);
16 flag = true;
17 }
18 }
19 }
20 }
21
22 public static void swap(int[] array, int m, int n) {
23 int temp = array[m];
24 array[m] = array[n];
25 array[n] = temp;
26 }
27 }
1 public class SelectSort {
2 public static void main(String[] args) {
3 int[] array = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
4 selectSort(array);
5 System.out.println(Arrays.toString(array));
6 }
7
8 public static void selectSort(int[] array) {
9 for(int i = 0; i ) {
10 int min = i;
11 for(int j = i + 1; j ) {
12 if(array[min] > array[j]) {
13 min = j;
14 }
15 }
16 if(min != i) {
17 int temp = array[min];
18 array[min] = array[i];
19 array[i] = temp;
20 }
21 }
22 }
23
24 public static void swap(int[] array, int m, int n) {
25 int temp = array[m];
26 array[m] = array[n];
27 array[n] = temp;
28 }
29 }
1 public class InsertSort {
2
3 public static void main(String[] args) {
4 int[] array = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
5 insertSort(array);
6 System.out.println(Arrays.toString(array));
7 }
8
9 public static void insertSort(int[] array) {
10 int j;
11 for(int i = 1; i ) {
12 if(array[i] ]) {
13 int temp = array[i];
14 for(j = i - 1; j >= 0 && array[j] > temp; j--) {
15 array[j + 1] = array[j];
16 }
17 array[j + 1] = temp;
18 }
19 }
20 }
21 }
1 public class ShellSort {
2
3 public static void main(String[] args) {
4 int[] array = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
5 shellSort(array);
6 System.out.println(Arrays.toString(array));
7 }
8
9 public static void shellSort(int[] array) {
10 int increment = array.length;
11 int j;
12 do {
13 increment = increment/3 +1;
14 for(int i = increment; i ) {
15 if(array[i] increment]) {
16 int temp = array[i];
17 for(j = i - increment; j >= 0 && array[j] > temp; j -= increment) {
18 array[j + increment] = array[j];
19 }
20 array[j + increment] = temp;
21 }
22 }
23 } while(increment > 1);
24 }
25 }
1 public class HeapSort {
2
3 public static void main(String[] args) {
4 int[] array = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
5 heapSort(array);
6 System.out.println(Arrays.toString(array));
7 }
8
9 public static void heapSort(int[] array) {
10 for (int i = array.length / 2; i > 0; i--) {//构建成大顶锥
11 heapAdjust(array, i, array.length);
12 }
13 for (int i = array.length - 1; i > 0; i--) {
14 int temp = array[0];
15 array[0] = array[i];
16 array[i] = temp;
17 heapAdjust(array, 1, i); //重新调整为大顶堆
18 }
19 }
20
21 public static void heapAdjust(int[] array, int s, int m) {
22 int temp, i, largest; //largest中存关键字较大的记录下标
23 temp = array[s - 1]; //表示第s个节点
24 for (i = 2 * s; i ) {
25 if (i array[i]) {
26 largest = i;
27 } else
28 largest = i - 1;
29 if (temp >= array[largest])
30 break;
31 array[s - 1] = array[largest];
32 s = largest + 1;
33 }
34 array[s - 1] = temp;
35 }
36 }
1 public class MeargeSort {
2
3 public static void main(String[] args) {
4 int[] array = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
5 mergeSort(array, 0, array.length - 1);
6 System.out.println(Arrays.toString(array));
7 }
8
9 public static void mergeSort(int[] array, int start, int end) {
10 if(start end) {
11 int mid = (start + end)/2;
12 mergeSort(array, start, mid);
13 mergeSort(array, mid + 1, end);
14 merge(array, start, mid, end);
15 }
16 }
17
18 public static void merge(int[] array, int s, int m, int e) {
19 int i, j, k;
20 int[] temp = new int[array.length];
21 for(i = s, j = m + 1, k = s; i ) {
22 if(array[i] array[j]) {
23 temp[k] = array[i++];
24 } else {
25 temp[k] = array[j++];
26 }
27 }
28 if(i m) {
29 for(int l = 0; l ) {
30 temp[k + l] = array[i + l];
31 }
32 }
33 if(j e) {
34 for(int l = 0; l ) {
35 temp[k + l] = array[j + l];
36 }
37 }
38 for(i = s; i ) {
39 array[i] = temp[i];
40 }
41 }
42 }
1 public class CycleMergeSort {
2
3 public static void main(String[] args) {
4 int[] array = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
5 mergeSort(array);
6 System.out.println(Arrays.toString(array));
7 }
8
9 public static void mergeSort(int[] array) {
10 int width = 1;
11 while(width array.length) {
12 mergePass(array, width);
13 width *= 2;
14 }
15 }
16
17 public static void mergePass(int[] array, int width) {
18 int start = 0;
19 while(start + 2 * width -1 array.length) {
20 merge(array, start, start + width -1, start + 2 * width -1);
21 start = start + 2 * width;
22 }
23 if(start + width -1 array.length) {
24 merge(array, start, start + width -1, array.length - 1);
25 }
26 }
27
28 public static void merge(int[] array, int s, int m, int e) {
29 int i, j, k;
30 int[] temp = new int[array.length];
31 for(i = s, j = m + 1, k = s; i ) {
32 if(array[i] array[j]) {
33 temp[k] = array[i++];
34 } else {
35 temp[k] = array[j++];
36 }
37 }
38 if(i m) {
39 for(int l = 0; l ) {
40 temp[k + l] = array[i + l];
41 }
42 }
43 if(j e) {
44 for(int l = 0; l ) {
45 temp[k + l] = array[j + l];
46 }
47 }
48 for(i = s; i ) {
49 array[i] = temp[i];
50 }
51 }
52 }
1 public class Qsort {
2
3 public static void main(String[] args) {
4 int[] array = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
5 Qsort(array, 0, array.length -1);
6 System.out.println(Arrays.toString(array));
7 }
8
9 public static void Qsort(int[] array, int low, int height) {
10 if(low height) {
11 int povit = partition(array, low, height);
12 Qsort(array, low, povit - 1);
13 Qsort(array, povit + 1, height);
14 }
15 }
16
17 public static int partition(int[] array, int low, int height){
18 int povit = array[low];
19 while(low height) {
20 while(low = povit) {
21 height--;
22 }
23 swap(array, low, height);
24 while(low povit) {
25 low++;
26 }
27 swap(array, low, height);
28 }
29 return low;
30 }
31
32 public static void swap(int[] array,int a, int b) {
33 int temp = array[a];
34 array[a] = array[b];
35 array[b] = temp;
36 }
37 }