javascript/js实现 排序二叉树数据结构 学习随笔
2020-12-13 04:56
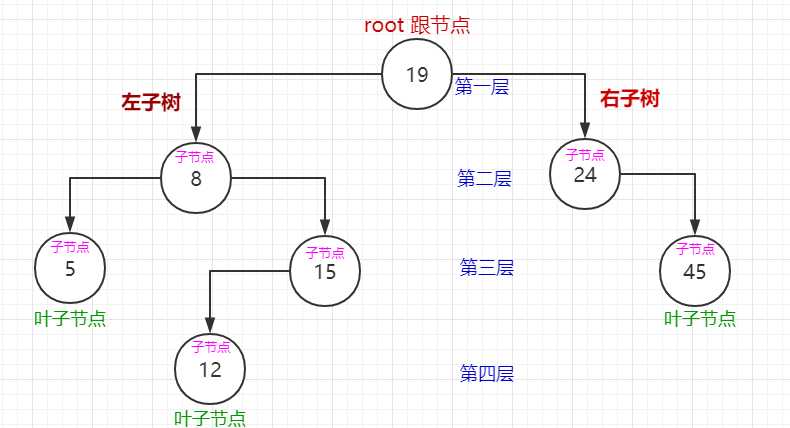
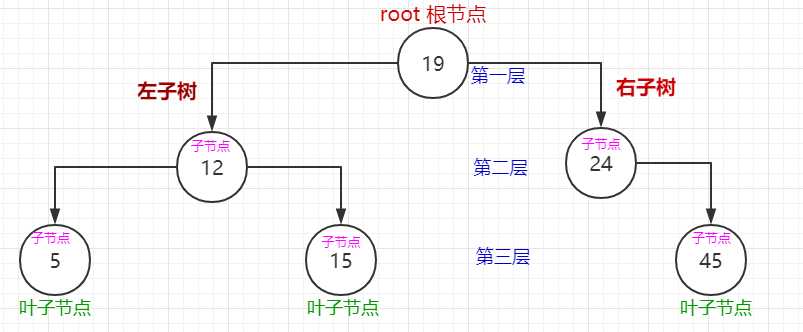
标签：存在 数据 代码实现 后序遍历 rip 结构 bsp OLE 结果 1.由一系列节点组成，具有层级结构。每个节点的特性包含有节点值、关系指针。节点之间存在对应关系。 2.树中存在一个没有父节点的节点，叫做根节点。树的末尾存在一系列没有子节点的节点，称为叶子节点。其他可以叫做中间节点。 3.树的根节点位于第一层，层级数越大，节点位置越深，层级数也叫做树高。 1.节点分为左右子树。 2.在不为空的情况下，左子树子节点的值都小于父节点的值。 3.在不为空的情况下，右子树子节点的值都大于父节点的值。 4.每个节点的左右子树都按照上述规则排序。 如图： 1.节点用对象来描述，节点特性用对象属性来描述。 2.二叉树结构用对象来描述。 相关方法： 具体用法： 结果： （1）以上图为例，中序遍历顺序为： 5 - 8 - 12 - 15 - 19 - 24 - 45。 （2）总是先遍历左子树，然后访问根节点，接着遍历右子树。 代码实现： 输入结果：5 - 8 - 12 - 15 - 19 - 24 - 45 （1）以上图为例，前序遍历顺序为： 19 - 8 - 5 - 15 - 12 - 24 - 45。 （2）总是先访问根节点，然后遍历左子树，接着遍历右子树。 代码实现： 输入结果：19 - 8 - 5 - 15 - 12 - 24 - 45 （1）以上图为例，后序遍历顺序为： 5 - 12 - 15 - 8 - 45 - 24 - 19。 （2）先遍历左子树，接着遍历右子树，最后访问根节点。 代码实现： 输入结果：5 - 12 - 15 - 8 - 45 - 24 - 19 代码实现： 结果： 代码实现： 结果： 根据排序二叉树的特点，比较给定值与节点值，小于时进入节点左子树。大于时进入节点右子树。等于时返回真。层层对比，最后如果子树为空，则表示没有找到。 代码实现： 结果： 当删除的节点为叶子节点时，直接把叶子节点设置成空。如图：删除值为5的节点。 原： 现： 当删除的节点存在左子树时，把父节点的关系指针直接指向左子树。如图：删除值为15的节点。存在右子树时同理。 原： 现： 当节点存在左右子树时，先去右子树里找到最小值，然后用最小值替换节点值，最后进入右子树删除最小值对应的节点。如图：删除值为8的节点。 原： 现： 代码实现： 结果： 累死我了。。。 javascript/js实现 排序二叉树数据结构 学习随笔 标签：存在 数据 代码实现 后序遍历 rip 结构 bsp OLE 结果 原文地址：https://www.cnblogs.com/caimuguodexiaohongmao/p/11123933.html二叉树是一种数据结构。其特点是：
排序二叉树为二叉树的一种类型，其特点是：
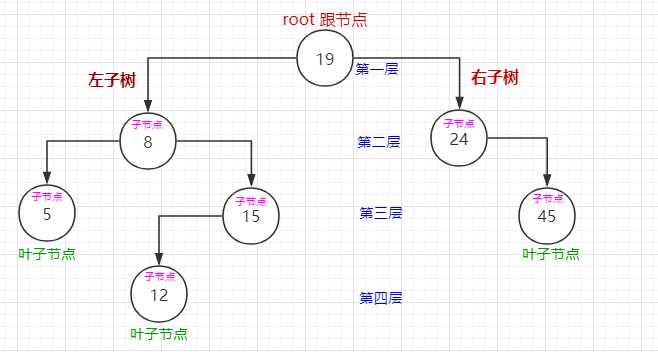（打错字了..）js代码来实现上述数据结构：
1 class Node {
2 constructor(key) {
3 this.key = key;// 节点值
4 this.left = null;// 左指针
5 this.right = null;// 右指针
6 }
7 }
1 // 二叉树
2 class BinaryTree {
3 constructor() {
4 this.root = null;// 根节点
5 }
6 insert(key) {// api--插入
7 const newNode = new Node(key);
8 if (this.root === null) {// 设置根节点
9 this.root = newNode;
10 }
11 method.insertNode(this.root, newNode);
12 }
13 }
1 // method
2 method = {
3 insertNode(root, newNode) {
4 if (newNode.key // 进入左子树
5 if (root.left === null) {// 左子树为空
6 root.left = newNode;
7 } else {// 左子树已存在
8 method.insertNode(root.left, newNode);
9 }
10 } else if (newNode.key > root.key) {// 进入右子树
11 if (root.right === null) {// 右子树为空
12 root.right = newNode;
13 } else {// 右子树已存在
14 method.insertNode(root.right, newNode);
15 }
16 }
17 }
18 };
1 // 实例化二叉树
2 const binaryTree = new BinaryTree();
3
4 // key值
5 const keys = [19, 8, 15, 24, 45, 12, 5];
6
7 // 生成排序二叉树
8 keys.forEach(key => binaryTree.insert(key));
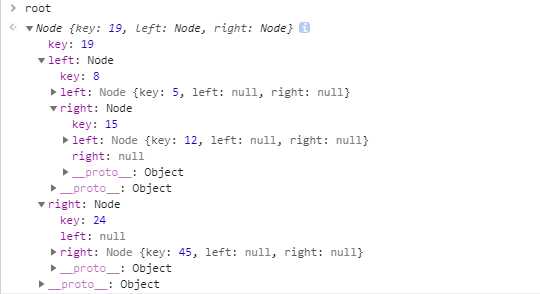
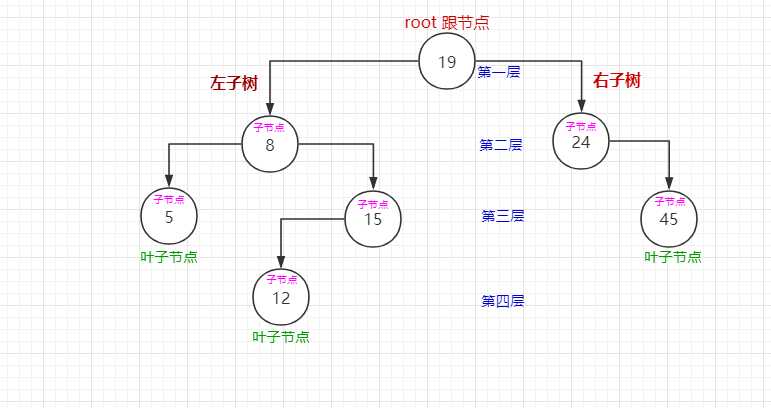
排序二叉树的遍历：
一、中序遍历
1 class BinaryTree {
2 ...
3 // callback为访问节点时执行的操作
4 inorderTraversal(callback) {// api--中序遍历
5 method.inorderTraversalNode(this.root, callback);
6 }
7 }
8
9 method = {
10 ...
11
12 inorderTraversalNode(node, callback) {
13 if (node) {// 当前节点
14 method.inorderTraversalNode(node.left, callback);// 遍历左子树
15 callback(node);// 访问节点
16 method.inorderTraversalNode(node.right, callback);// 遍历右子树
17 }
18 },
19 };
20
21 // 中序遍历
22 binaryTree.inorderTraversal(node => console.log(node.key));
1 // key值
2 const keys = [19, 8, 15, 24, 45, 12, 5];
二、前序遍历
1 class BinaryTree {
2 ...
3 preOrderTraversal(callback) {// api--前序遍历
4 method.preOrderTraversalNode(this.root, callback);
5 }
6 }
7
8 method = {
9 ...
10 preOrderTraversalNode(node, callback) {
11 if (node) {// 当前节点
12 callback(node);// 访问节点
13 method.preOrderTraversalNode(node.left, callback);// 遍历左子树
14 method.preOrderTraversalNode(node.right, callback);// 遍历右子树
15 }
16 }
17 };
18
19 // 前序遍历
20 binaryTree.preOrderTraversal(node => console.log(node.key));
1 // key值
2 const keys = [19, 8, 15, 24, 45, 12, 5];
三、后序遍历
1 class BinaryTree {
2 ...
3 postOrderTraversal(callback) {// api--后序遍历
4 method.postOrderTraversalNode(this.root, callback);
5 }
6 }
7
8 method = {
9 ...
10 postOrderTraversalNode(node, callback) {
11 if (node) {// 当前节点
12 method.postOrderTraversalNode(node.left, callback);// 遍历左子树
13 method.postOrderTraversalNode(node.right, callback);// 遍历右子树
14 callback(node);// 访问节点
15 }
16 }
17 };
18
19 // 后序遍历
20 binaryTree.postOrderTraversal(node => console.log(node.key));
1 // key值
2 const keys = [19, 8, 15, 24, 45, 12, 5];
排序二叉树的查找：
（1）查找最大值。根据排序二叉树的特点，右子树的值都大于父节点的值。只需要进入节点的右子树查找，当某个节点的右子树为空时，该节点就是最大值节点。
1 class BinaryTree {
2 ...
3 max() {
4 return method.maxNode(this.root);
5 }
6 }
7
8 method = {
9 ...
10 maxNode(node) {
11 if (node) {
12 while(node.right !== null) {// 右子树不为空时
13 node = node.right;
14 }
15 return node.key;
16 }
17 return null;
18 }
19 };
1 // key值
2 const keys = [19, 8, 15, 24, 45, 12, 5];
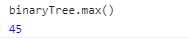
（2）查找最小值。根据排序二叉树的特点，左子树的值都小于父节点的值。只需要进入节点的左子树查找，当某个节点的左子树为空时，该节点就是最小值节点。
1 class BinaryTree {
2 ...
3 min() {
4 return method.minNode(this.root);
5 }
6 }
7
8 method = {
9 ...
10 minNode(node) {
11 if (node) {
12 while(node.left!== null) {// 左子树不为空时
13 node = node.left;
14 }
15 return node.key;
16 }
17 return null;
18 }
19 };
1 // key值
2 const keys = [19, 8, 15, 24, 45, 12, 5];
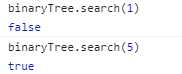
（3）查找给定值。在排序二叉树中查找有没有节点对应的值与给定值相同。
1 class BinaryTree {
2 ...
3 search(key) {
4 return method.searchNode(this.root, key);
5 }
6 }
7
8 method = {
9 ...
10 searchNode(node, key) {
11 if (node === null) {// 没有找到
12 return false;
13 }
14 if (key node.key) {// 进入左子树
15 return method.searchNode(node.left, key);
16 } else if (key > node.key) {// 进入右子树
17 return method.searchNode(node.right, key);
18 } else {// 找到了
19 return true;
20 }
21 }
22 };
1 // key值
2 const keys = [19, 8, 15, 24, 45, 12, 5];
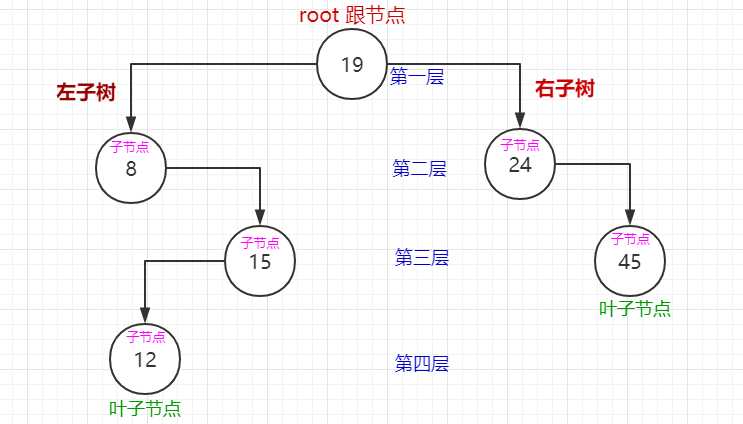
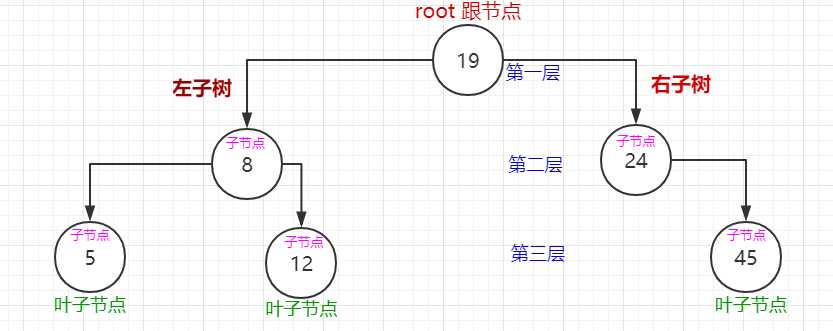
排序二叉树的删除：
1 class BinaryTree {
2 ...
3 remove(key) {
4 this.root = method.removeNode(this.root, key);
5 }
6 }
7
8 method = {
9 ...
10 removeNode(node, key) {
11 if(node === null) {// 没有找到值对应的节点
12 return null;
13 }
14 if (key // 给定值小于当前节点值
15 node.left = method.removeNode(node.left, key);
16 return node;
17 } else if (key > node.key) {// 给定值大于当前节点值
18 node.right = method.removeNode(node.right, key);
19 return node;
20 } else {// 找到给定值对应的节点
21 if (node.left === null && node.right === null) {// 节点为叶子节点
22 node = null;
23 return node;
24 }
25
26 if (node.left === null) {// 节点存在右子树
27 node = node.right;
28 return node;
29 } else if (node.right === null) {// 节点存在左子树
30 node = node.left;
31 return node;
32 }
33
34 // 节点存在左右子树时，先去右子树里找到最小值，然后用最小值替换节点值，最后进入右子树删除最小值对应的节点。
35 const minKey = method.minNode(node.right);
36 node.key = minKey;
37 method.removeNode(node.right, minKey);
38 return node;
39 }
40 }
41 };
上一篇：php(一)
文章标题：javascript/js实现 排序二叉树数据结构 学习随笔
文章链接：http://soscw.com/index.php/essay/30219.html