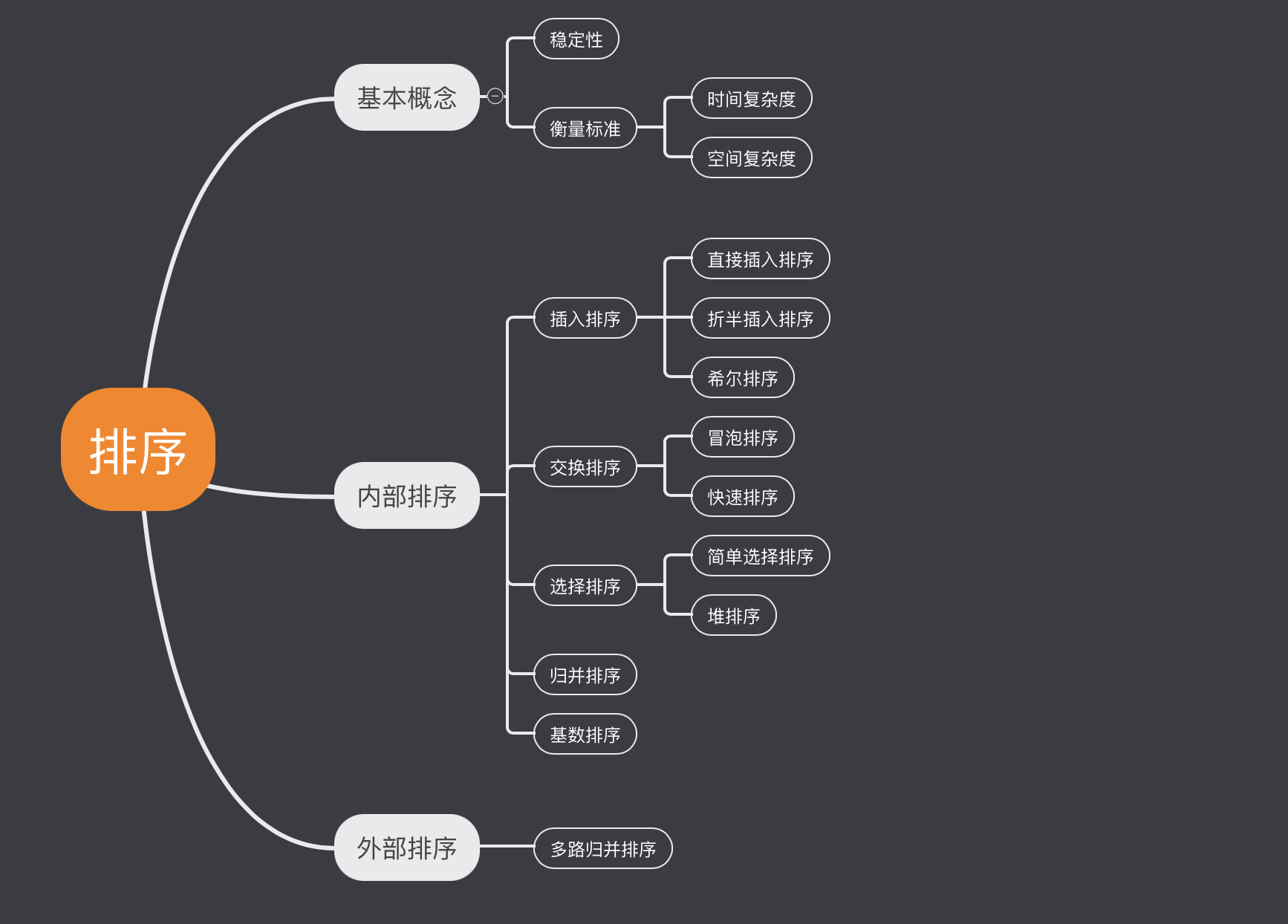
内部排序
2021-03-14 19:31
标签:i+1 链表 i++ shellSort 增量排序 line 有序 原来 数组 插入排序的思想是,假定前面i个元素已经有序,然后针对于第i+1个元素,寻找第i+1个元素应该在的位置,插入,移动即可 哨兵: 直接插入排序中(不管有没有哨兵的存在,其实是进行了两项工作) 在该算法中,总是一边比较,一边插入元素,下面将比较操作与移动操作进行分离,即现折半查找出元素的待插入位置,然后统一的移动待插入位置之后的所有元素。 直接插入排序适用于数组基本有序的数组的以及数据量不大的排序 希尔排序的思想: 算法过程 至今为止,没有一个最好的增量序列,一般情况下d1 = n/2,d2 = d1/2,并且最后一个增量为1 基数排序又称之为桶排序 排序算法小结 内部排序 标签:i+1 链表 i++ shellSort 增量排序 line 有序 原来 数组 原文地址:https://www.cnblogs.com/botak/p/13948825.html内部排序
插入排序
直接插入排序
没有哨兵的直接插入排序
public static void insertSort(int arr[]){
// 插入排序的思想是,假定前面i个元素已经有序,然后针对于第i+1个元素,寻找第i+1个元素应该在的位置,插入,移动即可
int len = arr.length;
int i;
int j;
// 遍历第1个到最后一个元素,假定第0个元素已经有序
for(i = 1;i带有哨兵的直接插入排序
public static void insertSort2(int[] arr){
int len = arr.length;
int i;
int j;
for(i = 2;i折半插入排序
public static void inHalfInsertSort(int[] arr){
int i;
int j;
int low;
int high;
int mid;
int len = arr.length;
// i从1开始,同直接排序的想法一样,假设第0个元素是有序的
for(i = 1;i希尔排序
希尔排序又称之为缩小增量排序
public static void shellSort(int[] arr){
int len = arr.length;
int i;
int j;
// 缩小增量的选取,也就是步数的选择
for(int step = len/2;step>=1;step=step/2){
// 对每一组的元素进行直接插入排序
for(i=step;i交换排序
冒泡排序
public static void bubbleSort(int[] arr){
// 冒泡排序类似于金鱼吐泡泡,比较两个相邻的元素,将大的元素放在后面
int len = arr.length;
// 进行len-1 次就结束了循环
for(int i = len;i>=0;i--){
// 设计一个标记位,如果没有元素进行移动就说明到达了最终的排序好的位置,就直接break
boolean flag = false;
for(int j = 0;j快速排序
public static void quickSort(int[] arr,int low,int high){
int left = low;
int right = high;
int pivot = arr[left];
if(low选择排序
简单选择排序
public static void selectSort(int[] arr){
// 选择排序
int len = arr.length;
for(int i = len-1;i>=0;i--){
int index = i;
for(int j = 0;j arr[index]) index = j;
}
int tmp = arr[i];
arr[i] = arr[index];
arr[index] = tmp;
}
print(arr);
}
堆排序
public static void heapSort(int[] arr){
// heap,使用java中的PriorityQueue默认是小顶堆,若要使用大顶堆,需要PriorityQueue(o1,o2->(o2-o1))
PriorityQueue归并排序
// 归并排序
public static void mergeSort(int[] arr,int low,int high){
int mid = (low+high)/2;
if(low基数排序

// 基数排序(桶排序)
// max表示数组中最大的位数有几位
public static void baseSort(int[] arr,int max){
// count 用来计数
int[] count = new int[arr.length];
// bucket用来当作桶,桶用来放数据,取数据
int[] bucket = new int[arr.length];
// k表示第几位,1代表个位,2代表十位,3代表百位
for(int k = 1;k排序比较
算法种类
时间复杂度(最好,平均,最差)
空间复杂度
是否稳定
直接插入排序
\(O(n)\),\(O(n^2)\),\(O(n^2)\)
\(O(1)\)
yes
希尔排序
\(O(1)\)
no
冒泡排序
\(O(n)\),\(O(n^2)\),\(O(n^2)\)
\(O(1)\)
yes
快速排序
\(O(n\log_2n)\),\(O(n\log_2n)\),\(O(n^2)\)
\(O(n\log_2n)\)
no
简单选择排序
\(O(n^2)\),\(O(n^2)\),\(O(n^2)\)
\(O(1)\)
no
堆排序
\(O(n\log_2n)\),\(O(n\log_2n)\),\(O(n\log_2n)\)
\(O(1)\)
no
归并排序
\(O(n\log_2n)\),\(O(n\log_2n)\),\(O(n\log_2n)\)
\(O(n)\)
yes
基数排序
O(r)
yes
排序算法应用
All coding
// 各种排序算法
import java.util.Arrays;
import java.util.PriorityQueue;
import java.util.List;
class Test{
public static void main(String[] args) {
int[] arr = new int[]{6,2,4,1,7,3,5};
print(arr);
// insertSort(arr);
// insertSort2(arr);
// inHalfInsertSort(arr);
// shellSort(arr);
// bubbleSort(arr);
// quickSort(arr,0,arr.length-1);
// print(arr);
// selectSort(arr);
// heapSort(arr);
// mergeSort(arr,0,arr.length-1);
int[] arr2 = {21,56,88,195,354,1,35,12,6,7};
baseSort(arr2,3);
}
// 打印数组
public static void print(int[] arr){
for(int i:arr) System.out.print(i+" ");
System.out.println();
}
// 直接插入排序,没有哨兵
public static void insertSort(int arr[]){
// 插入排序的思想是,假定前面i个元素已经有序,然后针对于第i+1个元素,寻找第i+1个元素应该在的位置,插入,移动即可
int len = arr.length;
int i;
int j;
// 遍历第1个到最后一个元素,假定第0个元素已经有序
for(i = 1;i
下一篇:java中list和map详解